Statistik-Crashkurs für CGM-Nutzer

Bei der Diabetestherapie, insbesondere bei der Nutzung eines Sensors (CGM), fallen eine Menge Daten an, die in den Apps (Dexcom Clarity) dann ausgewertet und mit statistischen Kennwerten dargestellt werden.
Statistische Standardangaben und leicht zu verstehen sind dabei Minimum (Min, der kleinste gemessene Wert) und Maximum (Max, der größte gemessene Wert).
Wichtiger und etwas komplizierter sind aber die durchschnittlichen Werte (Lageparameter, die das Zentrum der Verteilung beschreiben) und die zu diesen Durchschnitten passenden Streuungsmaße, die wiedergeben, wie weit die Einzelwerte von dem Durchschnittswert entfernt liegen (streuen).
Die gebräuchlichsten Durchschnittswerte sind dabei der arithmetische Mittelwert mit der Standardabweichung als dazugehörigem Streuungsmaß und der Median (Zentralwert) mit dem Interquartilsabstand als Streuungsmaß.

arithmetischer Mittelwert (x̅)

Der arithmetische Mittelwert (kurz: Mittelwert, ugs.: Durchschnitt (-swert)) errechnet sich, indem man die Summe der Einzelwerte (hier z.B. Glukosewerte) durch deren Anzahl dividiert.

Beispiel: 220, 100, 130, 110, 90 mg/dl (5 Werte)
Summe der Werte: 220 + 100 + 130 + 110 + 90 = 650
Mittelwert (Summe der Werte dividiert durch Anzahl der Werte): 650 ÷ 5 = 130 mg/dl

Median (Zentralwert)

Beim Median (Zentralwert) muss man zuerst die Werte der Urliste nach ihrer Größe ordnen. Bei der sortierten Liste ist der Median der Wert, der genau in der Mitte liegt. Bei einer geraden Anzahl von Werten ist der Median der Durchschnitt (die Hälfte) der beiden Werte, die in der Mitte liegen.

Beispiel Urliste: 220, 100, 130, 110, 90 mg/dl
geordnete Liste: 90, 100, 110, 130, 220 mg/dl
Median (Zentralwert): 110 mg/dl

Unterschiede Mittelwert - Median

In dem hier verwendeten Zahlenbeispiel liegt der Median bei 110 mg/dl und weicht vom Mittelwert (130 mg/dl) nach unten ab. Das ist bei Glukosewerten nicht verwunderlich: Bei einem Zielbereich von 70-180 mg/dl hat der Glukosewert nach unten (linke Seite) kaum einen Spielraum für Extremwerte (ab 40 mg/dl wird es für den Diabetiker kritisch), während nach oben (rechte Seite) viel Platz ist. Es kommen auch Werte über 300 mg/dl vor. Die Verteilungskurve steigt somit auf der linken Seite steil an, während sie auf der rechten Seite langsam abfällt. Es handelt sich also um eine schiefe Verteilung (Fachbegriff: rechtsschiefe bzw. linkssteile Verteilung). Während bei einer symmetrischen Verteilung die verschiedenen Mittelwerte (nahezu) identisch sind, gilt bei einer rechtsschiefen Verteilung: Modus (am häufigsten vorkommender Wert) < Median (Zentralwert) < arithmetisches Mittel.

Standardabweichung

"Die Standardabweichung ist ein Maß für die Streubreite der Werte eines Merkmals rund um dessen Mittelwert (arithmetisches Mittel). Vereinfacht gesagt, ist die Standardabweichung die durchschnittliche Entfernung aller gemessenen Ausprägungen eines Merkmals vom Durchschnitt. ... Die Berechnung der Standardabweichung erfolgt über die Quadratwurzel der Varianz. ... Die Standardabweichung besitzt immer die gleiche Maßeinheit wie das zu untersuchende Merkmal. Dadurch ist im Vergleich zur Varianz eine Interpretation einfacher. Eine kleinere Standardabweichung gibt in der Regel an, dass die gemessenen Ausprägungen eines Merkmals eher enger um den Mittelwert liegen, eine größere Standardabweichung gibt eine stärkere Streuung an. Für normalverteilte Merkmale gilt die Faustformel, dass innerhalb der Entfernung einer Standardabweichung nach oben und unten vom Mittelwert rund 68 Prozent alle Antwortwerte liegen. Im Umkreis von zwei Standardabweichungen sind es rund 95 Prozent aller Werte." (Quelle: externer Link ). Da ich es nicht besser formulieren kann, lasse ich das Zitat einfach so stehen. Ziel in der Diabetestherapie ist es natürlich die Standardabweichung (Streubreite der Glukosemesswerte) so klein wie möglich zu halten.
Wer weitere Details zur Berechnung wissen möchte, erhält hier noch die Definition von Varianz (Quelle ebenfalls statista.com): "Die Varianz ist ein Streuungsmaß, welches die Verteilung von Werten um den Mittelwert kennzeichnet. ... Berechnet wird die Varianz, indem die Summe der quadrierten Abweichungen aller Messwerte vom arithmetischen Mittel durch die Anzahl der Messwerte dividiert wird."

IQR (interquartile range, dt. IQA Interquartilsabstand)

In einem Quartil (Viertel) liegen jeweils 25% der nach Größe geordneten Messwerte. Dabei bezeichnet man als unteres Quartil die 25% der Messwerte, die unterhalb, und als oberes Quartil die 25%, die oberhalb des Medians liegen. Unteres und oberes Quartil zusammen ergeben den Interquartilsabstand (50% der Messwerte, die beidseits des Medians liegen). Der Interquartilsabstand ist das am wenigsten für Ausreißer (Extremwerte) anfällige Streuungsmaß.
Bei den Dexcom Clarity-Auswertungen zu den einzelnen Wochentagen und zu den einzelnen Stunden ist neben dem Medianwert die untere Grenze des unteren Quartils (Quartil 25) und die obere Grenze des oberen Quartils (Quartil 75) angegeben. Die Differenz zwischen "Quartil 75" und "Quartil 25" ergibt den Interquartilsabstand (IQR).
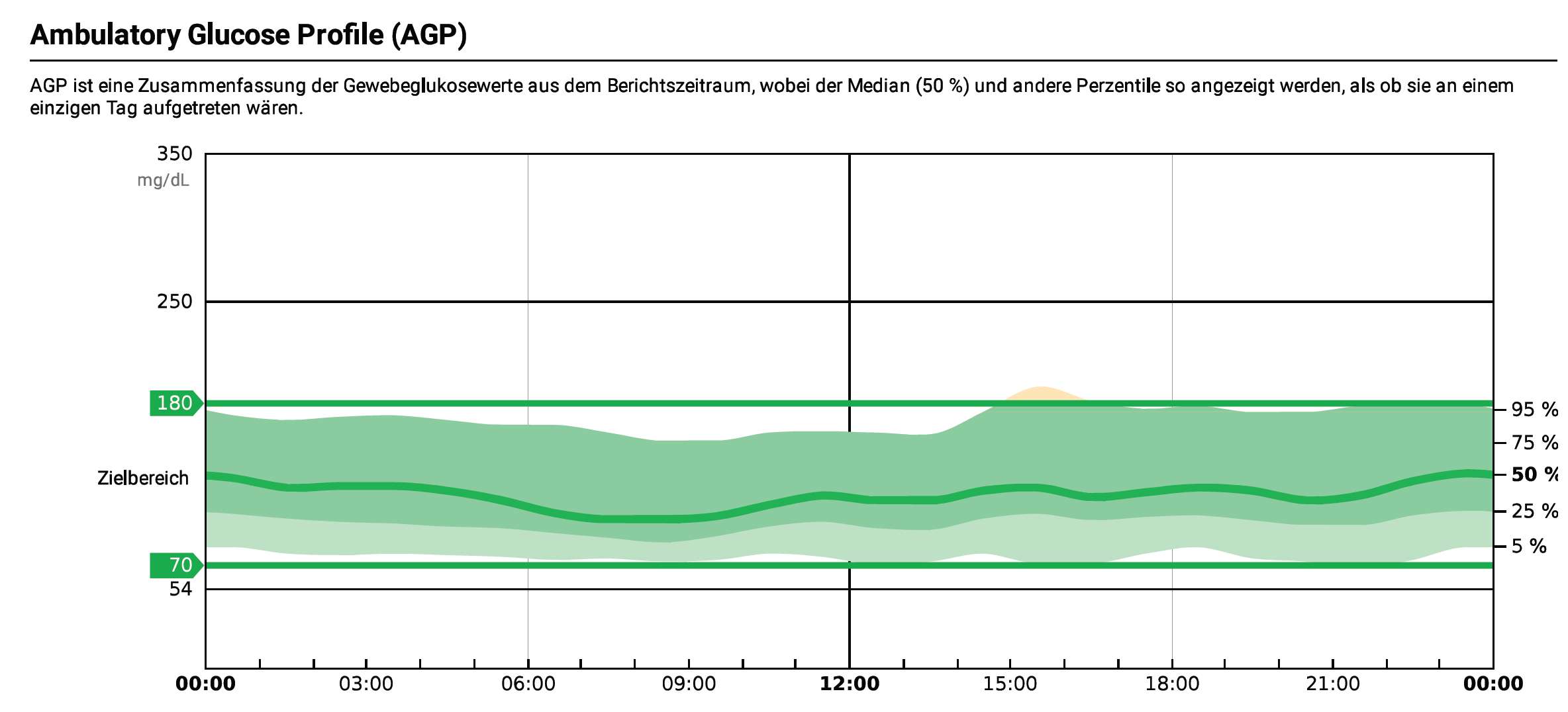
Bei der AGP-Statistik (Ambulatory Glucose Profile, ambulantes Glukoseprofil) sind in der Grafik das untere (25%) und obere Quartil (75%) farblich abgesetzt und zusätzlich noch der Bereich eingezeichnet, in dem 90% aller Messwerte liegen (5% ... 95%-Perzentile). Es werden dabei nur die Ausreißer (5% der niedrigsten und 5% der höchsten Werte) außer Acht gelassen.

zurück